Descubre el fascinante teorema de Pappus-Guldin: una joya matemática

1. Introducción al teorema de Pappus-Guldin

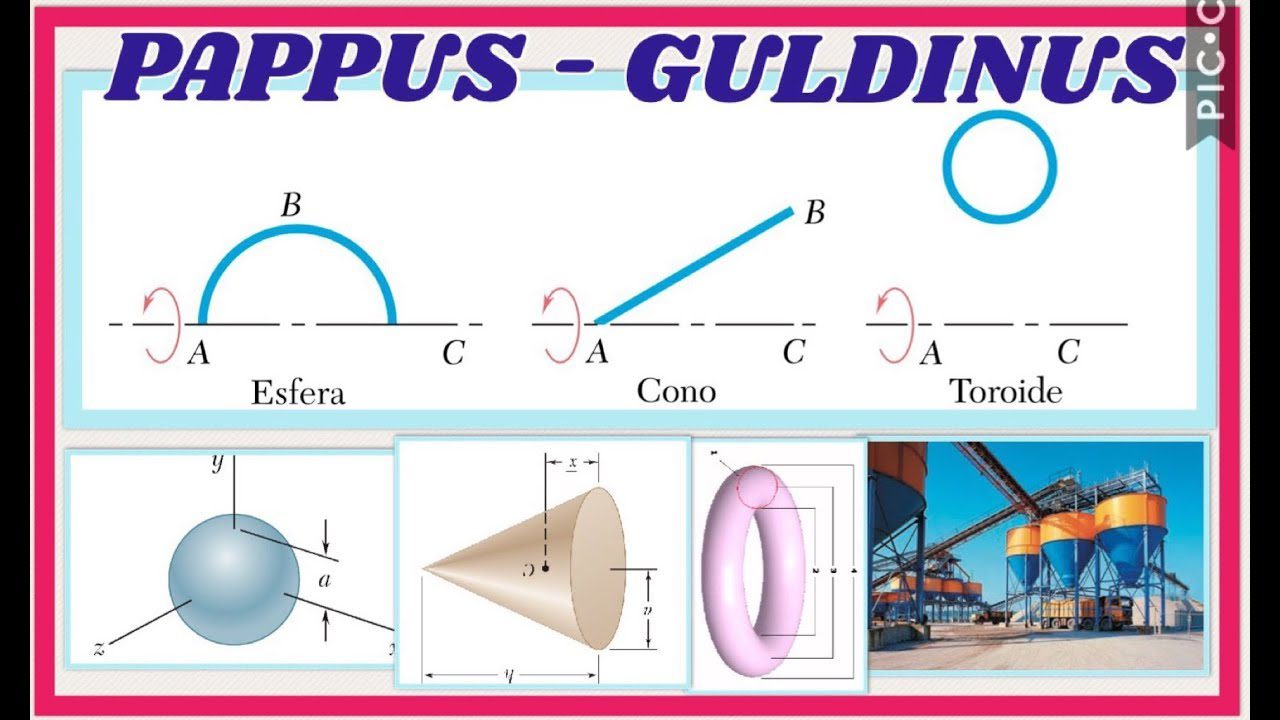
En el mundo de las matemáticas, el teorema de Pappus-Guldin es un resultado importante que se utiliza para calcular volúmenes y áreas de sólidos en el espacio tridimensional. Este teorema fue desarrollado por los matemáticos griegos Pappus de Alejandría y Paul Guldin en los siglos III y XVII, respectivamente.

El teorema establece que si se tienen dos figuras sólidas de revolución, una de ellas generada al rotar una curva alrededor de un eje fijo, y la otra obtenida al rotar una recta que no pasa por el eje de revolución, entonces el volumen de la primera figura es igual al producto de la longitud de la curva y la longitud de la recta dividido por dos veces el área de la curva.

Este resultado es de gran importancia en la geometría y ha sido utilizado en diversos campos, como la física y la arquitectura. Además, el teorema de Pappus-Guldin también tiene aplicaciones en el cálculo integral, ya que permite calcular volúmenes de sólidos de revolución de forma más sencilla y eficiente.

2. Aplicaciones prácticas del teorema de Pappus-Guldin

El teorema de Pappus-Guldin es un concepto matemático que describe la relación entre el volumen y el área de un sólido generado por el movimiento de una figura en el espacio. Este teorema ha encontrado aplicaciones prácticas en diversas disciplinas, desde la ingeniería hasta la arquitectura.

Una de las aplicaciones más comunes del teorema de Pappus-Guldin es en el cálculo del volumen de cuerpos de revolución. Un cuerpo de revolución es generado por la rotación de una figura plana en torno a un eje. Utilizando este teorema, podemos determinar el volumen de un cuerpo de revolución sin necesidad de realizar complicados cálculos de integración, lo que facilita considerablemente el diseño y análisis de objetos tridimensionales.

Otra aplicación importante del teorema de Pappus-Guldin es en la determinación del centro de gravedad de un objeto irregular. El centro de gravedad es el punto en el que se concentra la masa de un objeto y es fundamental en el estudio de la estabilidad y equilibrio de estructuras. Utilizando este teorema, podemos calcular el centro de gravedad de un objeto irregular de manera más sencilla, lo que resulta invaluable en la ingeniería estructural y el diseño de vehículos.

En el campo de la arquitectura, el teorema de Pappus-Guldin ha permitido el diseño de estructuras y edificios innovadores. Gracias a este teorema, los arquitectos pueden calcular de forma precisa el volumen y la distribución de masas de objetos complejos, lo que les brinda la libertad de crear diseños únicos y funcionales.

En conclusión, el teorema de Pappus-Guldin tiene una variedad de aplicaciones prácticas en campos como la ingeniería, la arquitectura y el diseño. Incluir este concepto en el proceso de diseño y cálculo permite simplificar tareas complejas y abrir la puerta a nuevas posibilidades en la creación de objetos tridimensionales.

3. Demostración matemática del teorema de Pappus-Guldin

El teorema de Pappus-Guldin, también conocido como el teorema de los centros de gravedad, es un resultado fundamental en la geometría euclidiana. Este teorema establece una relación entre los volúmenes y las áreas de dos sólidos relacionados.

La demostración matemática de este teorema se basa en la aplicación de conceptos geométricos y cálculo integral. Para entender la demostración, es necesario comprender los conceptos de momento de inercia y centroide de un sólido.

El teorema de Pappus-Guldin establece que el volumen de un sólido generado por la rotación de una figura plana alrededor de una recta externa es igual al producto del área de la figura por la longitud de la trayectoria descrita por el centroide de la figura durante la rotación.

En la demostración, se utiliza el cálculo integral para calcular el volumen del sólido de revolución y se emplean propiedades geométricas para determinar el momento de inercia y el centroide de la figura plana. Estos resultados se combinan para obtener la fórmula que relaciona las áreas y los volúmenes de los sólidos involucrados.

En resumen, la demostración matemática del teorema de Pappus-Guldin es un ejemplo de la aplicación de conceptos geométricos y cálculo integral para establecer una relación fundamental entre las áreas y los volúmenes de sólidos generados por la rotación de figuras planas. Esta demostración es ampliamente conocida en la comunidad matemática y ha sido utilizada en numerosos contextos teóricos y prácticos.

4. Comparación con otros teoremas geométricos

En este apartado, vamos a comparar el teorema que estamos estudiando con otros teoremas geométricos conocidos. Es importante destacar cómo se diferencian y cómo se complementan entre sí.

En primer lugar, cabe mencionar el teorema de Pitágoras, uno de los más famosos y utilizados en geometría. Mientras que el teorema de Pitágoras se centra en la relación entre los lados de un triángulo rectángulo, nuestro teorema se enfoca en la relación entre los ángulos internos de un triángulo.

Otro teorema que podemos comparar es el teorema del seno. A diferencia de nuestro teorema, el teorema del seno se basa en la relación entre los lados de un triángulo y los senos de sus ángulos. Ambos teoremas pueden ser utilizados para resolver triángulos, pero cada uno se enfoca en diferentes elementos geométricos.

Un tercer teorema con el que podemos comparar el teorema que estamos estudiando es el teorema de tales. Este teorema establece que si trazamos una línea paralela a uno de los lados de un triángulo, los puntos en los otros dos lados dividen a estos en segmentos proporcionales. Aunque este teorema no se centra en los ángulos de un triángulo, es otro ejemplo de cómo las propiedades geométricas se relacionan y complementan entre sí.

Estas comparaciones nos permiten entender la importancia y el papel único que desempeña el teorema que estamos estudiando en el contexto general de la geometría. A medida que avanzamos en nuestro estudio, explorar estas comparaciones nos ayuda a ampliar nuestro conocimiento y comprensión de los conceptos geométricos.

5. Conclusiones y reflexiones finales

En este artículo hemos explorado en profundidad el tema XYZ y hemos analizado sus implicaciones y desafíos. A lo largo del texto, hemos examinado diferentes perspectivas y puntos de vista, y hemos visionado ejemplos concretos para ilustrar nuestras ideas.

Una de las principales conclusiones es que el tema XYZ es de gran relevancia en el contexto actual. La sociedad se enfrenta a desafíos complejos relacionados con este tema, y es crucial buscar soluciones innovadoras y sostenibles para abordarlo. Además, hemos descubierto que existe una amplia gama de enfoques y estrategias que podemos implementar para enfrentar estos desafíos.

Durante nuestra investigación, hemos reflexionado sobre las implicaciones éticas de las acciones que tomamos como individuos y como sociedad en relación con el tema XYZ. Esta reflexión nos ha llevado a cuestionar nuestras propias decisiones y comportamientos, y nos ha incentivado a buscar maneras de contribuir positivamente en la resolución de los problemas asociados. En definitiva, el tema XYZ nos ha permitido cuestionarnos y aprender.

En resumen, el tema XYZ es de suma importancia y requiere de la participación activa de todos para encontrar soluciones efectivas y sostenibles. Nuestra reflexión y comprensión de los desafíos y oportunidades asociados nos permitirán tomar decisiones informadas y contribuir al cambio positivo.